Aufgaben
- Ist die Funktion
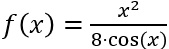symmetrisch zur x-Achse? - Prüfen Sie die Funktion f(x)=x·cos(x) auf Punktsymmetrie zum Ursprung.
- Begründen Sie, dass Funktion f(x)=sin(x-2)+3 punktsymmetrisch zum Punkt P(2|3) ist.
- Überprüfe, ob f(x)=4·e-0,25·(x2-6x+9)·cos(x-3) achsensymmetrisch ist zur Achse x=3.
Lösung Aufgabe 1.
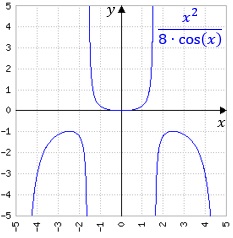
Es gilt
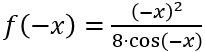.Da cos(x) symmetrisch zur x-Achse ist, gilt cos(-x)=cos(x).
Zusammen mit (-x)2=x2 erhält man:
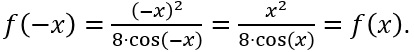
Ergebnis: f(x) ist symmetrisch zur x-Achse.
Lösung Aufgabe 2.
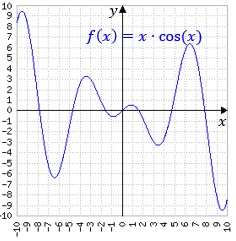
Es gilt f(-x)=(-x)·cos(-x)=-x·cos(x).
Beachte, dass cos(-x)=cos(x) ist.
Außerdem gilt -f(x)=-x·cos(x).
Wie man sieht ist f(-x)=-f(x).
Ergebnis: f(x) ist punktsymmetrisch zum Ursprung.
Lösung Aufgabe 3.
Durch Verschieben der Sinus-Funktion um 2 Einheiten nach rechts und um 3 Einheiten nach oben erhält man den Funktionsterm f(x)=sin(x-2)+3. Da die Sinus-Funktion punktsymmetrisch zum Ursprung ist, muss f(x) punktsymmetrisch zum Punkt P(2|3) sein.
Lösung Aufgabe 4.
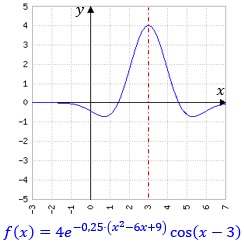
Es gilt
f(x)=4e(-0,25(x2-6x+9)·cos(x-3)=4e-0,25(x-3)2·cos(x-3)
Verschiebung um 3 nach links (also in die x-Achse) liefert:
g(x)=f(x+3)=4e-0,25x2·cos(x).
Nun ist g(-x)=4e-0,25(-x)2·cos(-x)=4e-0,25x2·cos(x)=g(x).
Das bedeutet, dass g(x) symmetrisch zur y-Achse ist und somit ist f(x) achsensymmetrisch zur Achse x=3!
Ergebnis: f(x) ist achsensymmetrisch zur Achse x=3.
| Downloads |
PowerPoint